For this case we have the following equations:

We must find
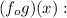
By definition of composition of functions we have to:
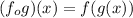
So:
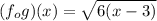
We must find the domain of f (g (x)). The domain will be given by the values for which the function is defined. That is to say:

Then, the domain is given by [3, ∞)
Answer:
The smallest number that is the domain of the composite function is 3