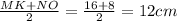Question

Given: MNOK is a trapezoid, MN=OK, m∠M=60°, NK⊥MN, MK=16cm
Find: The midsegment of MNOK

Answer 1

12 cm.

Explanation:

1. Consider right triangle MNK. In this triangle, angle N is right and m∠M=60°, then m∠K=30°. Thus, this triangle is a special 30°-60°-90° right triangle with legs MN and NK and hypotenuse MK=16 cm. The leg MN is opposite to the angle with a measure of 30°. This means that this leg is half of the hypotenuse, MN=8 cm.

2. Consider right triangle MNH, where NH is the height of trapezoid drawn from the point N. In this triangle m∠M=60°, angle H is right, then m∠N=30°. Similarly, the leg MH is half of the hypotenuse MN, MH=4 cm.

3. Trapezoid MNOK is isosceles because of MN=OK=8 cm. This means that NO=MK-2MH=16-8=8 cm.

4. The midsegment of the trapezoid is:

`(MK+NO)/(2)=(16+8)/(2)=12cm`

Answer 2

the length of the midsegment is 12 cm

Explanation:

ΔMNK is a 30°-60°-90° triangle, so side MK is twice the length of side MN. That makes MN = (16 cm)/2 = 8 cm.

Dropping an altitude from N to intersect MK at X, we have ΔMXN is also a 30°-60°-90° triangle with side MN twice the length of side MX. That makes MX = (8 cm)/2 = 4 cm.

The length of the midsegment of this isosceles trapezoid is the same as the length XK, so is (16 -4) cm = 12 cm.