Question

F(x)=10e-0.02x

This function represents the exponential decay of the bones of an extinct dinosaur in grams per year, where x is years. Using the graph, how many years does it take for the bones to be less than 5 grams?

Answer 1

35 years

Explanation:

We have been given an exponential decay function that models the weight of the bones of an extinct dinosaur;

`f(x)=10e^(-0.02x)`

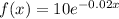
The initial weight of the bones is;

substitute x with 0 in the function, f(0) = 10 grams

We are required to determine the number of years it will take for the bones to be less than 5 grams. The solution can be achieved either analytically or graphically. I obtained the graph of the function from desmos graphing tool as shown in the attachment below.

From the graph, the bones will weigh 5 grams after approximately 34.65 years. This implies that it will take 35 years for the bones to be less than 5 grams.