Answer:
Option C is correct
Explanation:
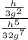
We need to simplify the above expression.
We can write the above expression as:
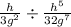
Changing division sign into multiplication and reciprocating the second term we get,
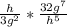
Applying the power rule: a^m/a^n = a^{m-n}
Solving:

So, Option C is correct.