Question

A building that is 100 for tall casts a shadow that makes a 30 degree angle. Approximately how long in feet is the shadow across the ground?

Answer 1

Hello!

The answer is:

The shadow is 173.20 feet

Why?

To solve the problem, we need to calculate the projection of the building's shadow over the ground.

We already know the height of the building (100 feet), also, we know the angle of elevation (30°), so, we can use the following formula to calculate it:

`Tan(\alpha)=(y)/(x)=(height)/(x)\\\\x=(height)/(Tan(\alpha) )`

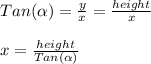
Now, substituting the given information and calculating, we have:

`x=(height)/(Tan(\alpha) )`

`x=(100feet)/(Tan(30\°) )=173.20feet`

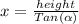
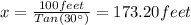
Have a nice day!

Answer 2

Answer: 173.20 ft

Explanation:

Observe the attached image. To know how long the shadow is, we must find the length of the adjacent side in the triangle shown. Where the opposite side represents the height of the building

By definition, the function
`tan (x)` is defined as

`tan(x) = (opposite)/(adjacent)`

So

`opposite = 100\ feet\\x=30\°`

`adjacent = l`

Then

`tan(30\°) = (100)/(l)`

`l = (100)/(tan(30\°))`

`l = 173.20\ ft`