Question

What is the solution of"​

Answer 1

Hence final answer is
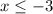`x \leq -3` or
`2 \leq x<7`

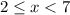
correct choice is A because both ends are open circles.

Explanation:

Given inequality is
`(x^2+x-6)/(x-7)\leq 0`

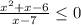
Setting both numerator and denominator =0 gives:

`x^2+x-6=0`, x-7=0

or
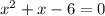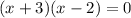`(x+3)(x-2)=0`, x-7=0

or x+3=0, x-2=0, x-7=0

or x=-3, x=2, x=7

Using these critical points, we can divide number line into four sets:

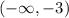`(-\infty,-3)`, (-3,2), (2,7),
`(7,\infty)`

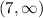
We pick one number from each interval and plug into original inequality to see if that number satisfies the inequality or not.

Test for
`(-\infty,-3)`.

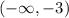Clearly x=-4 belongs to
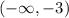`(-\infty,-3)` interval then plug x=-4 into
`(x^2+x-6)/(x-7)\leq 0`

`((-4)^2+(-4)-6)/((-4)-7)\leq 0`

`(6)/(-11)\leq 0`

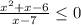
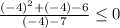
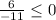
Which is TRUE.

Hence
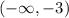`(-\infty,-3)` belongs to the answer.

Similarly testing other intervals, we get that only
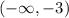`(-\infty,-3)` and
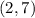`(2,7)` satisfies the original inequality.

Hence final answer is
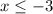`x \leq -3` or
`2 \leq x<7`

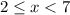
correct choice is A because both ends are open circles.