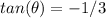Answer:
Part 1)
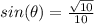
Part 2)
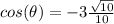
Part 3)
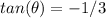
Explanation:
we know that
The angle is in the second quadrant so the sine is positive, the cosine is negative and the tangent is negative
step 1
Find the radius r applying the Pythagoras theorem
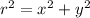
substitute the given values
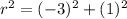
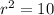
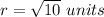
step 2
Find the value of
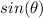
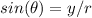
substitute values
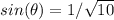
Simplify
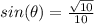
step 3
Find the value of
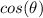
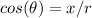
substitute values
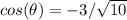
Simplify
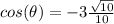
step 4
Find the value of
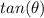
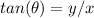
substitute values