Question

Points a,b, and c make the triangle ABC and are at the coordinates A(-2,9), B(-33,13) and c(-21,25) point D is the midpoint of BC and AD is a median of ABC, the equation of the median can be given by ax+by=c where A B and C

what is most simple way to answer this

Answer 1

`2x+5y=41`

Explanation:

Median of a triangle: A line segment that connects a vertex of a triangle to the midpoint of the opposite side.

Vertex: The point where any two sides of a triangle meet.

Given vertices of a triangle:

• A = (-2, 9)
• B = (-33, 13)
• C = (-21, 25)

Step 1

Find the midpoint of BC (Point D) by using the Midpoint formula.

Midpoint between two points

`\textsf{Midpoint}=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)\quad \textsf{where}\:(x_1,y_1)\:\textsf{and}\:(x_2,y_2)\:\textsf{are the endpoints}}\right)`

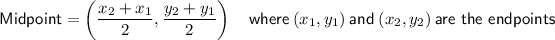
Define the endpoints:

• 
  `\text{Let }(x_1,y_1)=\sf B=(-33,13)`

• 
  `\text{Let }(x_2,y_2)=\sf C=(-21,25)`

Substitute the defined endpoints into the formula:

`\textsf{Midpoint of BC}=\left((-21-33)/(2),(25+13)/(2)\right)=(-27,19)`

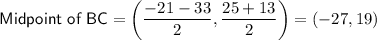
Therefore, D = (-27, 19).

Step 2

Find the slope of the median (line AD) using the Slope formula.

Define the points:

• 
  `\textsf{let}\:(x_1,y_1)=\sf A=(-2,9)`

• 
  `\textsf{let}\:(x_2,y_2)=\sf D=(-27,19)`

Substitute the defined points into the Slope formula:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(19-9)/(-27-(-2))=-(2)/(5)`

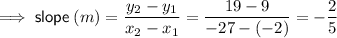
Therefore, the slope of the median is -²/₅.

Step 3

Substitute the found slope and one of the points into the Point-slope formula to create an equation for the median.

`\implies y-y_1=m(x-x_1)`

`\implies y-9=-(2)/(5)(x-(-2))`

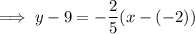
Simplify and rearrange the equation so it is in standard form Ax+By=C:

`\implies 5(y-9)=-2(x+2)`

`\implies 5y-45=-2x-4`

`\implies 2x+5y-45=-4`

`\implies 2x+5y=41`

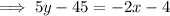
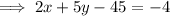
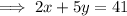
Conclusion

Therefore, the equation of the median is:

2x + 5y = 41