Question

For the geometric series
1+ 4+ 16 + 64 + 256
what is the value of n?

Answer 1

(n×4)

Explanation:

Divide the 2nd term by the first to find the ratio which is also n.

Answer 2

n=5.

Explanation:

The given geometric series is

1+ 4 +16 + 64 + 256

In the given G.P. the number of terms is 5 and n represents the number of terms in a G.P. So, n=5.

Alternate method:

Here the first term is 1 and the common ratio is

`r=(a_2)/(a_1)=(4)/(1)=4`

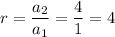
The nth term of a G.P. is

`a_n=ar^(n-1)`

where, a is first term and r is common ratio.

Substitute a=1, an=256 and r=4 in the above formula.

`256=(1)(4)^(n-1)`

`4^4=4^(n-1)`

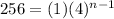
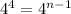
On comparing both sides we get

`4=n-1`

Add 1 on both sides.

`5=n`

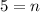
Therefore, the value of n is 5.