Question

Which functions have a y-intercept that is greater than the y-intercept of the function g(x) = |x + 3| + 4? Check three options.

f(x) = –2 (x – 8)2
h(x) = –5 |x| + 10
j(x) = –4(x + 2)2 + 8
k(x)=1/4(x-4)^2+4
m(x)=1/4 |x-8| +6

Answer 1

Answer with explanation:

The given function is

g(x)=|x+3|+4

The meaning of Y intercept is the distance between origin and Point where the curve cuts Y axis.

In , g(x), put x=0

g(0)=|0+3|+4

=3+4

=7

So, Length of Y intercept =7 unit

2.

f(x)=-2(x-8)²

f(0)=-2×(0-8)²

= -2 × 64

= -128

Length of Y intercept =-128 unit

3.

h(x)=-5|x|+10

h(0)=-5 × |0| +10

=10

Length of Y intercept =10 unit

4.

j(x)=-4(x+2)²+8

j(0)=-4×(0+2)²+8

=-4 × 4+8

= -16 +8

= -8

Length of Y intercept =-8 unit

4.

`\rightarrow k(x)=(1)/(4) * (x-4)^2+4\\\\\rightarrow k(0)=(1)/(4) * (0-4)^2+4\\\\\rightarrow k(0)= 4+4\\\\=8`

Length of Y intercept =8 unit

5.

`\rightarrow m(x)=(1)/(4) * |x-8|+6\\\\\rightarrow k(0)=(1)/(4) * |0-8|+6\\\\\rightarrow k(0)= 2+6\\\\=8`

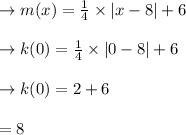
Length of Y intercept =8 unit

⇒ h(x),k(x) and m(x) has y intercept greater than y-intercept of the function g(x) = |x + 3| + 4.

Answer 2

h(x) = –5 |x| + 10

k(x)=1/4(x-4)^2+4

m(x)=1/4 |x-8| +6

Explanation:

The given function is:

g(x) = |x + 3| + 4

At y-intercept x=0,

g(0) = |0 + 3| + 4

g(0) = 3 + 4=7

The y-intercept of this function is 7.

We look for the functions with y-intercepts greater than 7.

`f(x)=-2(x-8)^2`

`f(0)=-2(0-8)^2`

`f(0)=-128`

h(x) = –5 |x| + 10

h(x) = –5 |0| + 10=10

`j(x)=-4(x+2)^2+8`

`j(0)=-4(0+2)^2+8=-8`

`k(x)=(1)/(4)(x-4)^2+4`

`k(0)=(1)/(4)(0-4)^2+4=8`

m(x)=1/4 |x-8| +6

m(0)=1/4 |0-8| +6=8