Question

The population of fish in a certain lake follows the logistic growth function , where t is the time in years.

When will the population reach 20,000?

Answer 1

46 years

Explanation:

We have the logistic growth function
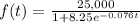`f(t)=(25,000)/(1+8.25e^(-0.076t))` and we want to find the time when the population will reach 20,000, to do it we just need to replace
`f(x)` with 20,000 and solve for
`t`:

`f(t)=(25,000)/(1+8.25e^(-0.076t))`

`20,000=(25,000)/(1+8.25e^(-0.076t))`

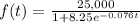
Divide both sides by 25,000

`(20,000)/(25,000) =(1)/(1+8.25e^(-0.076t))`

`0.8=(1)/(1+8.25e^(-0.076t))`

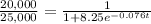
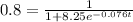
Multiply both sides by
`1+8.25e^(-0.076t)` and divide them by 0.8

`1+8.25e^(-0.076t)=1.25`

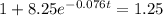
Subtract 1 from both sides

`8.25e^(-0.076t)=0.25`

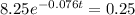
Divide both sides by 8.25

`e^(-0.076t)=(0.25)/(8.25)`

`e^(-0.076t)=(1)/(33)`

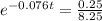
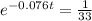
Take natural logarithm to both sides

`ln(e^(-0.076t))=ln((1)/(33) )`

`-0.076t=ln((1)/(33) )`

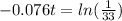
Divide both sides by -0.076

`t=(ln((1)/(33) ))/(-0.076)`

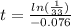
`t` ≈ 46

We can conclude that the population will reach 20,000 after 46 years.