Question

Nearing the end of his holiday preparations Richard has only one piece of Wrapping paper left for three remaining gifts. The remaining paper measures 25” x 45”. For gift a he needs to fi wrapping paper left for three remaining gifts. The remaining paper measures 25“ x 45“. For gift A he needs two-fifths of the wrapping paper. For gift B he needs one-third of wrapping paper.

Answer 1

Hello!

The answer is:

The dimensions of the paper for Gift C, are: 25" x 12"

and its area is:

`GiftCArea=300inch^(2)`

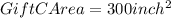
Why?

To solve the problem, we need to calculate the total area of the remaining paper, and then, subtract it from the paper used for the gift A and B.

We know that:

`GiftA=TotalPaperArea*(2)/(5)\\\\GiftB=TotalPaperArea*(1)/(3)`

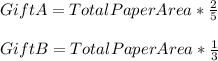
Now, the paper for Gift C will be:

`GiftCArea=(TotalPaperArea)-(PaperArea*(2)/(5)+PaperArea*(1)/(3))`

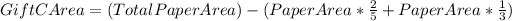
From the statement we know that the dimenstions of the remaining paper are 25" x 45", so calculating the area we have:

`TotalArea=25inch*45inch=1125inch^(2)`

Now, calculating the area of the paper for Gift A and B, we have:

`GiftA=1125inch^(2)*(2)/(5)=450inch^(2)\\\\GiftB=1125inch^(2)*(1)/(3)=375inch^(2)`

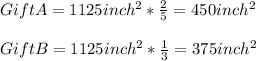
Then, calculating the paper for Gift C, we have:

`GiftCArea=(TotalPaperArea)-(PaperArea*(2)/(5)+PaperArea*(1)/(3))`

`GiftCArea=1125inch^(2)-(450inch^(2)+375inch^(2)+)`

`GiftCArea=1125inch^(2)-825inch^(2)=300inch^(2)`

`GiftCArea=300inch^(2)`

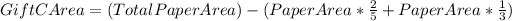
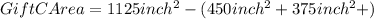
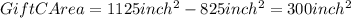
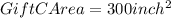
Therefore, calculating the dimensions of the paper for Gift C, knowing the height of the paper (25inches), we have::

`GiftCArea=Height*Width\\\\Width=(GiftCArea)/(25inches)=(300inches^(2) )/(25inches)=12inches`

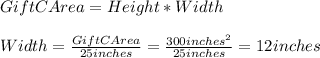
Hence, the dimensions of the paper for Gift C, are: 25" x 12".

Have a nice day!