Question

Which is the equation of the line that passes through (6, 2) and is perpendicular to a line with slope -1/3?

A. y-6=-1/3(x-2)
B. y-2=1/3(x-6)
C. y-2=3(x-6)
D. y-6=-3(x-2)
E. y-2=-3(x-6)

Answer 1

C

Explanation:

`( - 1)/(3) * a = -1`

then

`a = 3 \: where \: a \: is \: our \: line \: slope`

Answer 2

`\boxed{\text{C. } y - 2 = 3(x - 6)}`

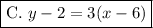
Explanation:

The slope of the perpendicular line m₂ must be the negative reciprocal of the slope m₁ of the first line.

`m_(2) = -(1)/(m_(1)) = -(1)/(-(1)/(3)) = 3`

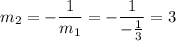
The only equation with m = 3 is

`\boxed{\textbf{C. } y - 2 = 3(x - 6)}`

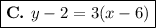
This is the point slope form of the equation for a straight line through (6, 2) with slope = 3.