Question

10 Points! Drag each value or expression to the correct location on the equations and sentences. Each value and expression can be used more than once, but not all values and expressions will be used.

Gary works at a bakery, and he needs to select a rectangular cookie sheet with an area of 192 square inches. The area of the cookie sheet is represented by the expression given below.


`x^(2) + 4x`

Complete the given statements, and find the width of the cookie sheet.

Answer 1

Hello!

The answers are:

Second step:

First box, 4

Second box,

The width is:

`x+4`

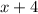
Fourth step:

Box, 16

The length cant be -16in, the length is 12in, and the width is 16in.

Why?

To solve the problem, we are using the formula to calculate the area of a rectangle, however, since the dimensions of the rectangle are not constant numbers, we will work with the variable "x", also, we know that the area of the cookie sheet is equal to 192 square inches.

So, solving we have:

First step:

We have the expression:

`x^(2) +x`

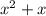
Which is equal to:
`192in^(2)`

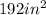
So,

`x^(2) +4x=492`

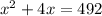
Second step:

We have that the common factor of the left side of the equation is "x", so, we can simplify the expression in the following way:

`x(x+4)=492`

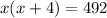
Now, using the formula to calculate the area of a rectangle, we have:

`length*width=Area\\\\length*width=92in^(2)\\\\x(x+4)=192in^(2)`

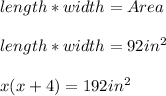
Where,

The length of the rectangle is "x"

The width of the rectangle is "x+4"

Third step:

Rewriting the expression, we have:

`x^(2) +4x-192=0`

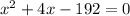
We need to find the roots (zeroes) of the quadratic function, in order to find the width of the rectangle without using the variable "x".

So, finding the values of "x" (roots or zeroes of the expression), we have:

`x^(2) +4x-192=0`

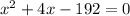
Fourth step:

We need to find two numbers which it product gives as result the number -192 (including its sign) and their algebraic sum gives as result "4", those numbers are, -12 and 16,

`-12*(16)=-192\\-12+16=4`

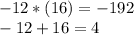
Then, rewriting the equation, we have:

`(x+16)(x-12)=0`

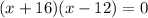
So, we that the expression is equal to 0 for two values of "x", these values are:

`x_1=-16\\x_2=12`

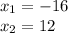
Now, since the length can't be -16in, its equal to 12in.

`length=x=12in`

`length=12`

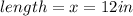
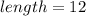
Then, from the second equation, we have that:

`width=x+4`

Substituting "x" we can find the value of the width, so:

`width=x+4=\\\\width=12+4=16in`

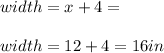
Hence, we have:

`length=12in\\width=16in`

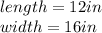
Have a nice day!