Question

Let a1, a2, a3, ... be a sequence of positive integers in arithmetic progression with common difference

2. Also, let b1, b2, b3, ... be a sequence of positive integers in geometric progression with common
ratio 2. If a1 = b1 = c, then the number of all possible values of c, for which the equality

2(a1 + a2 + ⋯ + an

) = b1 + b2 + ⋯ + bn

holds for some positive integer n, is _____

Answer 1

Since
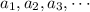`a_1,a_2,a_3,\cdots` are in arithmetic progression,

`a_2 = a_1 + 2`

`a_3 = a_2 + 2 = a_1 + 2\cdot2`

`a_4 = a_3+2 = a_1+3\cdot2`

`\cdots \implies a_n = a_1 + 2(n-1)`

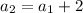
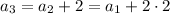
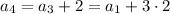
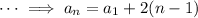
and since
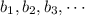`b_1,b_2,b_3,\cdots` are in geometric progression,

`b_2 = 2b_1`

`b_3=2b_2 = 2^2 b_1`

`b_4=2b_3=2^3b_1`

`\cdots\implies b_n=2^(n-1)b_1`

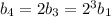
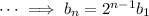
Recall that

`\displaystyle \sum_(k=1)^n 1 = \underbrace{1+1+1+\cdots+1}_(n\,\rm times) = n`

`\displaystyle \sum_(k=1)^n k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}2`

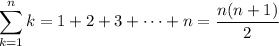
It follows that

`a_1 + a_2 + \cdots + a_n = \displaystyle \sum_(k=1)^n (a_1 + 2(k-1)) \\\\ ~~~~~~~~ = a_1 \sum_(k=1)^n 1 + 2 \sum_(k=1)^n (k-1) \\\\ ~~~~~~~~ = a_1 n +  n(n-1)`

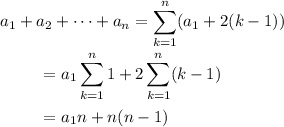
so the left side is

`2(a_1+a_2+\cdots+a_n) = 2c n + 2n(n-1) = 2n^2 + 2(c-1)n`

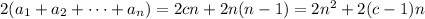
Also recall that

`\displaystyle \sum_(k=1)^n ar^(k-1) = (a(1-r^n))/(1-r)`

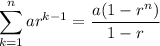
so that the right side is

`b_1 + b_2 + \cdots + b_n = \displaystyle \sum_(k=1)^n 2^(k-1)b_1 = c(2^n-1)`

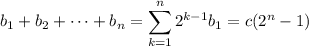
Solve for
`c`.

`2n^2 + 2(c-1)n = c(2^n-1) \implies c = (2n^2 - 2n)/(2^n - 2n - 1) = (2n(n-1))/(2^n - 2n - 1)`

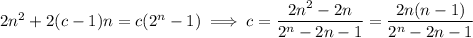
Now, the numerator increases more slowly than the denominator, since

`(d)/(dn)(2n(n-1)) = 4n - 2`

`(d)/(dn) (2^n-2n-1) = \ln(2)\cdot2^n - 2`

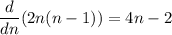
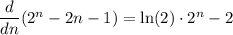
and for
`n\ge5`,

`2^n > \frac4{\ln(2)} n \implies \ln(2)\cdot2^n - 2 > 4n - 2`

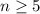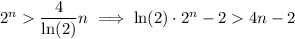
This means we only need to check if the claim is true for any
`n\in\{1,2,3,4\}`.

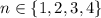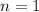`n=1` doesn't work, since that makes
`c=0`.

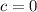If
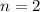`n=2`, then

`c = (4)/(2^2 - 4 - 1) = \frac4{-1} = -4 < 0`

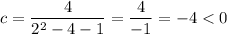
If
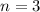`n=3`, then

`c = (12)/(2^3 - 6 - 1) = 12`

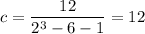
If
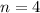`n=4`, then

`c = (24)/(2^4 - 8 - 1) = \frac{24}7 \\ot\in\Bbb N`

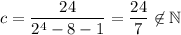
There is only one value for which the claim is true,
`c=12`.