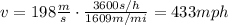Question

Imagine a raindrop starting from rest in a cloud 2 km in the air. If it fell with no air friction at all, it would accelerate toward the ground with gravitational acceleration of 9.8m/s2. What would the speed of the drop be when it reached the ground? Convert your answer into miles per hour.

1) 212 mph
2) 433 mph
3) 774 mph
4) 72.5 mph

Answer 1

2) 433 mph

Step-by-step explanation:

The final velocity of the raindrop as it reaches the ground can be found by using the equation for a uniformly accelerated motion:

`v^2 = u^2 + 2ad`

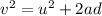
where

v is the final velocity

u = 0 is the initial velocity (the raindrop starts from rest)

a = g = 9.8 m/s^2 is the acceleration due to gravity

d = 2 km = 2000 m is the distance covered

Solving for v,

`v=√(u^2 +2gd)=√(0^2+2(9.8 m/s^2)(2000))=198 m/s`

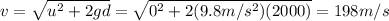
And keeping in mind that

1 mile = 1609 metres

1 hour = 3600 s

The speed converted into miles per hour is

`v=198 (m)/(s)\cdot (3600 s/h)/(1609 m/mi)=433 mph`