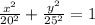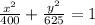Question

Write an equation in standard form of an ellipse that is 50 units high and 40 units wide. The center of the ellipse is (0,0).

Answer 1

`(x^2)/(400)+(y^2)/(625)=1`

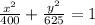
Explanation:

The equation of an ellipse that has its center at the origin is given by the formula:

`(x^2)/(b^2)+(y^2)/(a^2)=1`

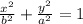
The given ellipse is 50 units high.

This means that length of the major axis is 50.

`2a=50`

`2\implies a=25`

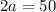
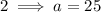
The ellipse is 40 units wide.

`2b=40`

`\implies b=20`

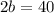
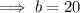
We substitute these values into the formula to get:

`(x^2)/(20^2)+(y^2)/(25^2)=1`

`(x^2)/(400)+(y^2)/(625)=1`