Answer:
f(x) = (x - 1)(x + 2)(x - 3)
Explanation:
We are given the following function and we are to factorize it completely:

To factorize this completely, we will use the rational roots theorem.
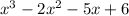
P = ± multiples of constant term
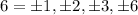
Q = ± multiples of the coefficient of highest degree term

So the factors will be
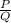 .
.
The possible rational roots are
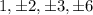 .
.
1 is a confirmed root and now we will use synthetic division to find the other rational roots:
1 | 1 -2 -5 6
1 -1 -6
___________
1 -1 -6 0
So the polynomial will be
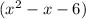 which can we factorize now.
which can we factorize now.

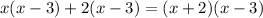
Therefore, the completely factorized form of the given function is f(x) = (x - 1)(x + 2)(x - 3).