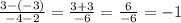Question

Find the slope of the line through (2, -3) and (-4, 3).

-1
0
1

Answer 1

-1

Explanation:

The slope of a line is the ratio of its change in rise to its change in run. In the -xy-plane, this is the same as the ratio of the change in y coordinate to the change in x coordinate. In notation, we write this as

`(\Delta y)/(\Delta x)`

and calculate it by finding the difference between y coordinates and dividing it by the difference between x coordinates. Here, our y coordinates are 3 and -3, and our x coordinates are -4 and 2, so our slope would be

`(3-(-3))/(-4-2)=(3+3)/(-6)=(6)/(-6)=-1`

Answer 2

-1

EXPLANATION

The slope formula is given by

`m = (y_1-y_2)/(x_1-x_2)`

The slope of the line through (2, -3) and (-4, 3) is found by substituting the points into the above formula;

`m = ( - 3 - 3)/(2 - - 4)`

This simplifies to

`m = ( - 6)/( 6) = - 1`

The slope is -1