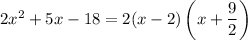Question

Pemfaktoran dari 2x²+5x-18

​

Answer 1

We can factor a polynomial by finding its roots. In particular, a quadratic equation has (at most) two roots
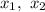`x_1,\ x_2`, which would allow us to write the polynomial as

`p(x)=a(x-x_1)(x-x_2)`

To find the solutions, we can use the quadratic formula

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a) = (-5\pm√(169))/(4) = (-5\pm13)/(4)`

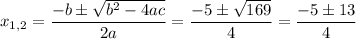
So, the two solutions are

`(-5+13)/(4) = 2\quad\text{and}\quad(-5-13)/(4) =-(9)/(2)`

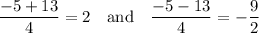
And so we can factor the polynomial as follows:

`2x^2+5x-18=2(x-2)\left(x+(9)/(2)\right)`