Question

Use Euler's Formula

2) vertices: 11
Edges: 34
Faces: ?
A: 25
B: 28
C: 26
D: 24

3: Edges: 36
Faces: 22
Vertices: ?
A: 19
B: 15
C: 16
D: 17

4) Faces: 12
Vertices: 10
Edges: ?
A: 23
B: 22
C: 25
D: 20

# 5 has a picture attached with the answer choices

If you help can you maybe explain how to do one of them for me it would really help me out a lot!

Answer 1

Part 2) Option A: 25

Part 3) Option C: 16

Part 4) Option D: 20

Part 5) pentagon

Explanation:

we know that

The Euler's formula state that, the number of vertices, minus the number of edges, plus the number of faces, is equal to two

so

`V- E+ F=2`

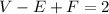
Part 2) we have

vertices: 11

Edges: 34

Faces: ?

substitute the values in the formula and solve for F

`11- 34+ F=2`

`-23+ F=2`

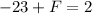
Adds 23 both sides

`F=2+23`

`F=25`

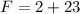
Part 3) we have

Edges: 36

Faces: 22

Vertices: ?

substitute the values in the formula and solve for V

`V- 36+ 22=2`

`V- 14=2`

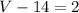
Adds 14 both sides

`V=2+14`

`V=16`

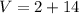
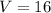
Part 4) we have

Faces: 12

Vertices: 10

Edges: ?

substitute the values in the formula and solve for E

`10- E+ 12=2`

`- E+ 22=2`

Subtract 22 both sides

`- E=2-22`

`- E=-20`

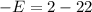
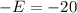
Multiply by -1 both sides

`E=20`

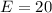
Part 5) we know that

The cross section of the figure is a plane figure with five straight sides and five angles

therefore

The figure is a pentagon