Question

Below are two different functions, f(x) and g(x). What can be determined about their y-intercepts?

f(x) = x + 4

x g(x)
−1 | 8
1 | 0
2 | −4

A) The function f(x) has a higher y-intercept.
B) The function g(x) has a higher y-intercept.
C) They both have the same y-intercept.
D) The relationship between y-intercepts cannot be determined.

Answer 1

D) The relationship between y-intercepts cannot be determined.

Explanation:

We have been given two different functions f(x) and g(x). Now we need to find about what can be determined about their y-intercepts. Then match with the correct choice from the given choices:

A) The function f(x) has a higher y-intercept.

B) The function g(x) has a higher y-intercept.

C) They both have the same y-intercept.

D) The relationship between y-intercepts cannot be determined.

We know that y-intercept is the y of function value when x=0.

In the table of g(x), we don't see any point that has x=0

So we can't find the y-intercept for g(x)

Hence correct choice is :

D) The relationship between y-intercepts cannot be determined.

Answer 2

Hello!

The answer is:

C) They both have the same y-intercept.

Why?

In order to find the correct option, we need to find the equation of the function g(x), and then, compare its y-intercept with the y-intercept of the f(x) function.

So,

- Finding the equation of the g(x):

Calculating the slope of the function, using the first two points (-1,8) and (1,0), we have:

`m=(y_2-y_1)/(x_2-x_1)\\\\m=(0-8)/(1-(-1))=(-8)/(2)=-4`

Now, calculating the value of "b" using the first point (-1,8) and the slope of the function, we have:

`y=mx+b`

`y=-x+b`

`8=-4(-1)+b`

`b=4`

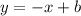
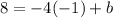
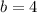
So, the equation of g(x) is:

`y=-4x+4`

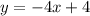
- Comparing the y-intercepts of f(x) and g(x):

Finding the y-intercept of f(x), by making "x" equal to 0, we have:

`y=x+4\\\\y=4`

We have that the function f(x) has its y-intercept at "y" equal to 4.

Finding the y-intercept of g(x), by making "x" equal to 0, we have:

`y=-4x+4`

`y=-4*(0)+4`

`y=4`

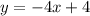
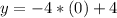
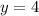
We have that the function g(x) has its y-intercept at "y" equal to 4.

Hence, we have that both functions have their y-intercepts at the same point, so, the correct option is:

C) They both have the same y-intercept.

Have a nice day!