Question

What is the average rate of change from x = −3 to x = −4?

Answer 1

-2

Explanation:

Since it would be immensely helpful to know the equation of this parabola, we need to figure it out before we can continue. We have the work form of a positive upwards-opening parabola as

`y=a(x-h)^2+k`

where a is the leading coefficient that determines the steepness of lack thereof of the parabola, x and y are coordinates of a point on the graph, and h and k are the coordinates of the vertex. We know the vertex: V(-3, -3), and it looks like the graph goes through the point P(-2, -1). Now we will fill in the work form equation and solve for a:

`-1=a(-2-(-3))^2-3`

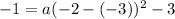
which simplifies a bit to

`-1=a(1)^2-3`

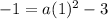
and

-1 = a(1) - 3. Therefore, a = 2 and our parabola is

`y=2(x+3)^2-3`

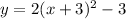
Now that know the equation, we can find the value of y when x = -3 (which is already given in the vertex) and the value of y when x = -4. Do this by subbing in the values of x one at a time to find y. When x = -3, y = -3 so the coordinate of that point (aka the vertex) is (-3, -3). When x = -4, y = -1 so the coordinate of that point is (-4, -1). The average rate of change between those 2 points is also the slope of the line between those 2 points, so we will use the slope formula to find it:

`m=(-1-(-3))/(-4-(-3)) =(2)/(-1)=-2`

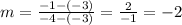
And there you have it! I'm very surprised that this question sat unanswered for so very long! I'm sorry I didn't see it earlier!