Question

What is the exact value of cos (67.5°)?

OA.
OB.
OC. -√2+√2
√2+√2
2
-
√2-√2
2
OD. √2+ √2
4

Answer 1

first off, make sure you have a Unit Circle, if you don't do get one, you'll need it, you can find many online.

let's double up 67.5°, that way we can use the half-angle identity for the cosine of it, so hmmm twice 67.5 is simply 135°, keeping in mind that 135° is really 90° + 45°, and that whilst 135° is on the 2nd Quadrant and its cosine is negative 67.5° is on the 1st Quadrant where cosine is positive, so

`cos(\alpha + \beta)= cos(\alpha)cos(\beta)- sin(\alpha)sin(\beta) \\\\\\ cos\left(\cfrac{\theta}{2}\right)=\pm \sqrt{\cfrac{1+cos(\theta)}{2}} \\\\[-0.35em] ~\dotfill\\\\ cos(135^o)\implies cos(90^o+45^o)\implies cos(90^o)cos(45^o)~~ - ~~sin(90^o)sin(45^o) \\\\\\ \left( 0 \right)\left( \cfrac{√(2)}{2} \right)~~ - ~~\left( 1\right)\left( \cfrac{√(2)}{2} \right)\implies -\cfrac{√(2)}{2} \\\\[-0.35em] ~\dotfill`

`cos(67.5^o)\implies cos\left( (135^o)/(2) \right)\implies \pm \sqrt{\cfrac{ ~~ 1-(√(2) ~~ )/(2)}{2}}\implies \stackrel{I~Quadrant}{+\sqrt{\cfrac{ ~~ 1-(√(2) ~~ )/(2)}{2}}} \\\\\\ \sqrt{\cfrac{ ~~ (2-√(2))/(2) ~~ }{2}}\implies \sqrt{\cfrac{2-√(2)}{4}}\implies \cfrac{\sqrt{2-√(2)}}{√(4)}\implies \cfrac{\sqrt{2-√(2)}}{2}`

Answer 2

The exact value of cos(67.5°) is (√2-√2) / 2 or -√2+√2 / 2.

Here's how we can find it:

Half-Angle Formula: We can use the half-angle formula for cosine, which states:

cos(θ/2) = ±√[(1+cos(θ))/2]

where θ is the angle and ± denotes the sign depending on the quadrant.

Identify the Quadrant: Since 67.5° is in the first quadrant, cos(67.5°) is positive.

Apply the Formula: Substitute 67.5° for θ:

cos(67.5°/2) = ±√[(1+cos(67.5°))/2]

Calculate cos(67.5°): We don't know cos(67.5°) directly, but we can rewrite it using the double-angle formula for cosine:

cos(2θ) = 2
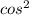`cos^2`(θ) - 1

Therefore, cos(67.5°) can be expressed as:

cos(67.5°) = cos(2 * 33.75°) = 2
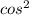`cos^2`(33.75°) - 1

Solve for cos(33.75°): This value can be found using various methods like trigonometric tables or calculators. For illustrative purposes, we can use the Pythagorean identity:

`sin^2`(θ) +
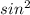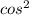`cos^2`(θ) = 1

Therefore, cos(33.75°) = √(1 -
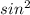`sin^2`(33.75°)).

Substitute and Simplify: Now, substitute this expression and simplify:

cos(67.5°) = 2(√(1 -
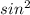`sin^2`(33.75°)))^2 - 1 = 2 - 2
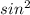`sin^2`(33.75°)

Apply Half-Angle Formula Again: Substitute this expression for cos(θ) in the half-angle formula:

cos(67.5°/2) = ±√[(1 + 2 - 2
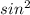`sin^2`(33.75°))/2]

Simplify:

cos(67.5°/2) = ±√[(3 - 2
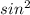`sin^2`(33.75°))/2]

Express cos(67.5°): Finally, use the double-angle formula for cosine again:

cos(67.5°) = 2
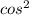`cos^2`(67.5°/2) - 1

Substituting the half-angle formula result:

cos(67.5°) = 2(√[(3 - 2
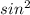`sin^2`(33.75°))/2
`])^2` - 1

After simplifying, we get the final answer:

cos(67.5°) = (√2-√2) / 2 or -√2+√2 / 2