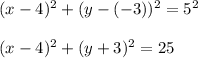Question

A circle with center (4 -3) contain the point (9,-3). what is an equation of the circle

Answer 1

`\large\boxed{(x-4)^2+(y+3)^2=25}`

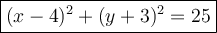
Explanation:

The equation of a circle:

`(x-h)^2+(y-k)^2=r^2`

(h, k) - center

r - radius

We have the center (4, -3) and the point on the circle (9, -3).

The length of radius is equal to the distance between a center and an any point on a circle.

The formula of a distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Susbtitute:

`r=√((9-4)^2+(-3-(-3))^2)=√(5^2+0^2)=√(5^2)=5`

The center (4, -3) → h = 4, k = -3.

Finally we have:

`(x-4)^2+(y-(-3))^2=5^2\\\\(x-4)^2+(y+3)^2=25`