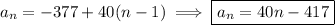Question

Please help with sequences and series problem!

Answer 1

In an arithmetic sequence, consecutive terms are separated by a common difference
`d` and are given recursively by

`a_n=a_(n-1)+d`

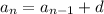
So we can write
`a_(51)` in terms of
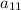`a_(11)` by substituting recursively:

`a_(51)=a_(50)+d`

`a_(51)=(a_(49)+d)+d=a_(49)+2d`

`a_(51)=(a_(48)+d)+2d=a_(48)+3d`

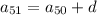
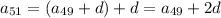
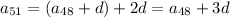
and so on up to

`a_(51)=a_(11)+40d`

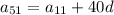
(notice how in
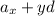`a_x+yd`, it's always true that
`x` and
`y` add up to 51)

We're given that
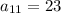`a_(11)=23` and
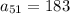`a_(51)=183`, so we can solve for
`d`:

`183=23+40d\implies40d=160\implies d=40`

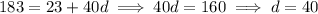
We can use the same strategy to find the first term in the sequence:

`a_(11)=a_(10)+40`

`a_(11)=(a_9+40)+40=a_9+80`

`a_(11)=(a_8+40)+80=a_8+120`

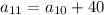
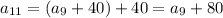
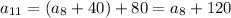
and so on up to

`a_(11)=a_1+400`

`23=a_1+400\implies a_1=-377`

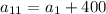
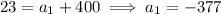
In general, the sequence has a pattern of

`a_n=a_(n-1)+40`

`a_n=(a_(n-2)+40)+40=a_(n-2)+2\cdot40`

`a_n=(a_(n-3)+40)+2\cdot40=a_(n-3)+3\cdot40`

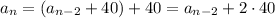
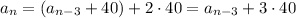
and so on up to

`a_n=a_1+(n-1)\cdot40`

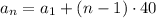
So this sequence is given by the rule

`a_n=-377+40(n-1)\implies \boxed{a_n=40n-417}`