Question

The focus of a parabola is (−5,−1) and the directrix is y=−3.

What is an equation of the parabola?


(x+5)^2=y+2

(x+5)^2=4(y+2)

(x+5)^2=2(y+5)

(x+5)^2=8(y+5)

Answer 1

(x+5)2=4(y+2)

Explanation:

Answer 2

The second choice down is the one you want

Explanation:

There's a couple of things to know about parabolas in this form before you can write the equation from information given. The first is that if the parabola opens upward or downward it is y = x^2 or y = -x^2. If it opens to the right or to the left it is a x = y^2 or x = -y^2 parabola. We can tell how it opens from the location of the focus and what type of directrix it has. First, a parabola wraps itself around the focus, and the way in which it wraps itself is dependent upon the equation of the directrix. A "y = " directrix means that the parabola opens up or down (again, it wil wrap itself around the focus) and an "x =" directrix means that the parabola opens to the right or to the left. Ok. Now. Our directrix is a "y =" equation, so the parabola opens either up or down. If we plot the focus and then draw in the directrix, we see that the focus is above the directrix, so the parabola opens upwards.

Because of this, the standard form for our parabola is:

`(x-h)^2=4p(y-k)`

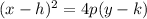
where h and k are the coordinates of the vertex and p is the distance between the vertex and the focus, or the vertex and the directrix. This distance is the same for both. That means that the vertex lies directly in between the focus and the directrix. Since our focus is (-5, -1) and the directrix is y = -3, then the vertex lies at a y-coordinate of -1, and will lie on the same x coordinate as does the focus. So that means our vertex is at (-5, -2). From this point we see that there is unit that separates it from both the focus and the directrix. That is our "p" value. Filling in our equation:

`(x+5)^2=4(1)(y+2)`

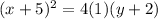
which of course simplifies to

`(x+5)^2=4(y+2)`

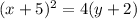
And there you go!