Question

A thick, spherical shell made of solid metal has an inner radius a = 0.18 m and an outer radius b = 0.46 m, and is initially uncharged. A point charge q = 5.00 C is placed at the center of the shell. What is the electric field strength in the region r < a? Express your answer in terms of 1/r2. Tries 0/8 What is the electric field strength in the region a < r < b? Express your answer in terms of 1/r2. Tries 0/8 What is the electric field strength in the region b < r? Express your answer in terms of 1/r2. Tries 0/8 What is the induced charge density at r = a? (in C/m^2) Tries 0/8 What is the induced charge density (in C/m2) at r = b?

Answer 1

(a)
`E(r) = (q)/(4\pi \epsilon_0 r^2)`

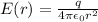
We can solve the different part of the problem by using Gauss theorem.

Considering a Gaussian spherical surface with radius r<a (inside the shell), we can write:

`E(r) \cdot 4\pi r^2 = (q)/(\epsilon_0)`

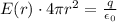
where q is the charge contained in the spherical surface, so

`q=5.00 C`

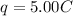
Solving for E(r), we find the expression of the field for r<a:

`E(r) = (q)/(4\pi \epsilon_0 r^2)`

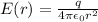
(b) 0

The electric field strength in the region a < r < b is zero. This is due to the fact that the charge +q placed at the center of the shell induces an opposite charge -q on the inner surface of the shell (r=a), while the outer surface of the shell (r=b) will acquire a net charge of +q.

So, if we use Gauss theorem for the region a < r < b, we get

`E(r) \cdot 4\pi r^2 = (q')/(\epsilon_0)`

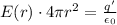
however, the charge q' contained in the Gaussian sphere of radius r is now the sum of the charge at the centre (+q) and the charge induced on the inner surface of the shell (-q), so

q' = + q - q = 0

And so we find

E(r) = 0

(c)
`E(r) = (q)/(4\pi \epsilon_0 r^2)`

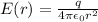
We can use again Gauss theorem:

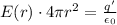`E(r) \cdot 4\pi r^2 = (q')/(\epsilon_0)` (1)

where this time r > b (outside the shell), so the gaussian surface this time contained:

- the charge +q at the centre

- the inner surface, with a charge of -q

- the outer surface, with a charge of +q

So the net charge is

q' = +q -q +q = +q

And so solving (1) we find

`E(r) = (q)/(4\pi \epsilon_0 r^2)`

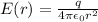
which is identical to the expression of the field inside the shell.

(d)
`-12.3 C/m^2`

We said that at r = a, a charge of -q is induced. The induced charge density will be

`\sigma_a = (-q)/(4\pi a^2)`

where
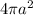`4 \pi a^2` is the area of the inner surface of the shell. Substituting

q = 5.00 C

a = 0.18 m

We find the induced charge density:

`\sigma_a = (-5.00 C)/(4\pi (0.18 m)^2)=-12.3 C/m^2`

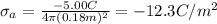
(e)
`-1.9 C/m^2`

We said that at r = b, a charge of +q is induced. The induced charge density will be

`\sigma_b = (+q)/(4\pi b^2)`

where
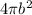`4 \pi b^2` is the area of the outer surface of the shell. Substituting

q = 5.00 C

b = 0.46 m

We find the induced charge density:

`\sigma_b = (+5.00 C)/(4\pi (0.46 m)^2)=-1.9 C/m^2`