Question

Can someone give me the answers to problems a-l? I already finished it but I don't have an answer key so I want to check with someone. Thanks.

Answer 1

If we approach 1 from the left, we're using the blue function, but if we approach 1 from the right, we're using the green function. So, we have

`\displaystyle \lim_(x\to 1^-)f(x) = 0,\quad\lim_(x\to 1^+)f(x) = -1`

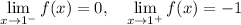
Since the left and right limits are different, the limit

`\displaystyle \lim_(x\to 1)f(x)`

does not exist.

When we approach 0, we always use the blue function. Both halves of the blue function tend to 1 as x approaches zero. So, in this case, we have

`\displaystyle \lim_(x\to 0^-)f(x) = \lim_(x\to 0^+)f(x) = 1 = \lim_(x\to 0)f(x)`

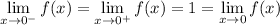
Note that the fact that, by definition, we have
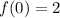`f(0)=2` doesn't mean that the limit is wrong, or that it doesn't exist. It simply means that the function is not continuous, because we have

`\displaystyle f(x_0)\\eq \lim_(x\to x_0)f(x)`

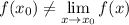
As for -2, x can approach this value only from the left, because the function is not defined between -2 and -1. So, we have

`\displaystyle \lim_(x\to -2)f(x) = \lim_(x\to -2^-)f(x) 0-\infty`

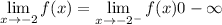
The limit as x approaches 3 is similar to the one where x approaches zero: the function is not defined at x=3, but the limit from both sides approaches -1:

`\displaystyle \lim_(x\to 3^-)f(x) = \lim_(x\to 3^+)f(x) = -1 = \lim_(x\to 3)f(x)`

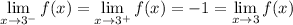
As for the limits as x approaches infinity, we have to deduce from the graph that the funtion grows indefinitely as x grows, i.e.

`\displaystyle \lim_(x\to +\infty)f(x) = +\infty`

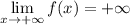
And that the function has no limit as
`x\to-\infty`, because it has a sinusoidal behaviour, with an ever-growing amplitude.