Question

Help asap!!!!

What is the length of the arc intercepted by a central angle of 62° on a circle with radius 8? Use 3.14 for π and round your answer to the nearest hundredth, if necessary.

7.25


9.11


8.65


7.82

Answer 1

8.65 is the answer to this question.

Answer 2

Option 3 - 8.65

Explanation:

Given : The arc intercepted by a central angle of 62° on a circle with radius 8.

To find : What is the length of the arc?

Solution :

The formula to find arc length is

`l=2\pi r* ((\theta)/(360^\circ))`

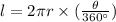
Where, l is the length of the arc

r is the radius of the circle r=8

`\theta=62^\circ` is the angle subtended

Substitute the values in the formula,

`l=2* 3.14* 8* ((62^\circ)/(360^\circ))`

`l=50.24* 0.1722`

`l=8.65`

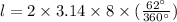
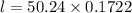
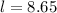
Therefore, option 3 is correct.

The length of the arc is 8.65 unit.