Answer:
1) 9/cos(θ)
2)4
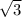 (cos(198) +isin(198))
(cos(198) +isin(198))
3)z= cos(π/3) +isin(π/3)
Explanation:
x=9
i.e. x= 9 +i0
θ= tan^-1 (0/9)
θ= tan^-1 (0)
=0
hence z= r(cosθ +i sinθ)
= 9(cos 0 + isin 0)
= 9
As cos (0) = 1 hence polar form of x=9 is 9/cos(θ) where θ=0
2)
Given
z1=2
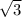 ( cos(116)+isin(116))
( cos(116)+isin(116))
z2=2(cos(82)+isin(82))
As per the product formula od complex polar numbers:
z1.z2= r1.r2(cos(θ1+θ2) +isin(θ1+θ2) )
Putting the values
= 4
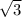 (cos(198) +isin(198))
(cos(198) +isin(198))
3)
z= 1/2 + i
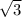 /2
/2
r=
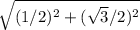
r =
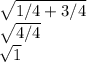
r=1
θ= tan^-1
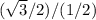
= tan^-1
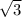
=60
=π/3
hence
z= cos(π/3) +isin(π/3) !