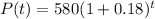Question

The initial count of a certain type of bacteria in a culture is 580. If the bacteria continually grow at the rate of 18% per hour, which function models the number of bacteria after t hours?

Answer 1

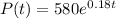`P (t) = 580e ^ {0.18t}` or
`P (t) = 580 (1.18) ^ t`

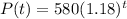
Explanation:

There are two models of exponential growth that you can use to predict the population of bacteria after t hours.

I)
`P (t) = pe ^ {rt}`

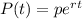
II)
`P (t) = p (1 + r) ^ t`

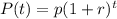
Where

p is the initial population of bacteria

r is the growth rate

t is the time in hours.

In this case we know that:

`p = 580\\\\r = (18)/(100)\\\\r = 0.18`

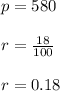
Then the equations that can be used to predict the population of bacteria after t hours are:

I)
`P (t) = 580e ^ {0.18t}`

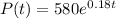
II)
`P (t) = 580 (1 + 0.18) ^ t`