Question

Triangle ABC is rotated 180 degrees around point B and then dilated to form triangle DBE as shown. Which postulate or theorem establishes that the triangles are similar? AA Similarity SSS Similarity SAS Similarity ASA Similarity

Answer 1

AAA Similarity

Explanation:

Given:

Triangles ABC and DBE

Required

Which postulate shows ABC and DBE similarity

From the question, we understand that the following transformation were done on ABC

1. Rotation
2. Dilation

It should be noted that, when a triangle (e.g. triangle ABC) is rotated, the length of the sides and angle measurements remain unchanged.

However, when this triangle is dilated, the sides of the triangle change, but the angles remain unchanged.

Having said that,

When ABC is rotated and dilated to form DBE, we have:

`\angle A = \angle D = a`

`\angle B = \angle B = b`

`\angle C = \angle E = c`

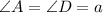
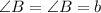
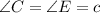
[See Attachment]

Hence, the postulate that answers this question is AAA (Angle-Angle-Angle).