Answer:
1) cos (3x)
2)
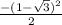
Explanation:
Given expression:
cos(7x)cos(4x)+sin(7x)sin(4x)
By using the trigonometric identity
cos(a)cos(b) + sin(a)sin(b) = cos(a-b)
we have:
cos(7x)cos(4x)+sin(7x)sin(4x) = cos(7x - 4x)
= cos(3x)!
part 2:
tan (-π/12)
by using property tan(-x)= - tan(x)
=-tan(π/12)
= - tan(π/6 / 2)
Using tan(x/2) =
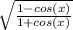
= -
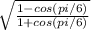
cos π/6 =
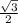
= -
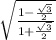
= -
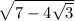
= - 2+
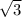
=
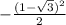
!