Question

PLEASE HELP ASAP!!! CORRECT ANSWER ONLY PLEASE!!!

Use technology or a z-score table to answer the question.

The lengths of green beans for sale at a supermarket are normally distributed with a mean of 11.2 centimeters and a standard deviation of 2.1 centimeters. Consider a bag of 150 green beans.

How many green beans will be 13 centimeters or shorter?

Answer 1

Choice C: approximately 121 green beans will be 13 centimeters or shorter.

Explanation:

What's the probability that a green bean from this sale is shorter than 13 centimeters?

Let the length of a green bean be
`X` centimeters.

`X` follows a normal distribution with

• mean
  `\mu = 11.2` and
• standard deviation
  `\sigma = 2.1`.

In other words,

`X\sim \text{N}(11.2, 2.1^(2))`,

and the probability in question is
`X \le 13`.

Z-score table approach:

Find the z-score of this measurement:

`\displaystyle z= (x-\mu)/(\sigma) = (13-11.2)/(2.1) = 0.857143`. Closest to 0.86.

Look up the z-score in a table. Keep in mind that entries on a typical z-score table gives the probability of the left tail, which is the chance that
`Z` will be less than or equal to the z-score in question. (In case the question is asking for the probability that
`Z` is greater than the z-score, subtract the value from table from 1.)

`P(X\le 13) = P(Z \le 0.857143) \approx 0.8051`.

"Technology" Approach

Depending on the manufacturer, the steps generally include:

• Locate the cumulative probability function (cdf) for normal distributions.
• Enter the lower and upper bound. The lower bound shall be a very negative number such as
  `-10^(9)`. For the upper bound, enter
  `13`
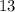
• Enter the mean and standard deviation (or variance if required).
• Evaluate.

For example, on a Texas Instruments TI-84, evaluating
`\text{normalcdf})(-1\text{E}99,\;13,\;11.2,\;2.1 )` gives
`0.804317`.

As a result,

`P(X\le 13) = 0.804317`.

Number of green beans that are shorter than 13 centimeters:

Assume that the length of green beans for sale are independent of each other. The probability that each green bean is shorter than 13 centimeters is constant. As a result, the number of green beans out of 150 that are shorter than 13 centimeters follow a binomial distribution.

• Number of trials
  `n`: 150.
• Probability of success
  `p`: 0.804317.

Let
`Y` be the number of green beans out of this 150 that are shorter than 13 centimeters.
`Y\sim\text{B}(150,0.804317)`.

The expected value of a binomial random variable is the product of the number of trials and the probability of success on each trial. In other words,

`E(Y) = n\cdot p = 150 * 0.804317 = 120.648\approx 121`

The expected number of green beans out of this 150 that are shorter than 13 centimeters will thus be approximately 121.