Answer:
z = -0.4.
Explanation:
Here's the formula for finding the z-score (a.k.a. standardized normal variable) of one measurement
 of a normal random variable
of a normal random variable
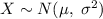 :
:
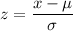 ,
,
where
 is the z-score of this measurement,
is the z-score of this measurement,
 is the value of this measurement,
is the value of this measurement,
 is the mean of the random normal variable, and
is the mean of the random normal variable, and
 is the standard deviation (the square root of variance) of the random normal variable.
is the standard deviation (the square root of variance) of the random normal variable.
Let the length of a trout in this lake be
 inches.
inches.
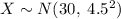 .
.
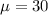 , and
, and
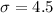 .
.
For this measurement,
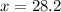 . Apply the formula to get the z-score:
. Apply the formula to get the z-score:
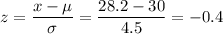 .
.