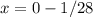Question

70 POINTS!!!!

Find the focus, directrix, and equation of the parabola in the graph.

Answer 1

B

Explanation:

Confirmed on E D G 2021

Answer 2

Option B

Part a) The focus is
`(1/28,0)`

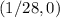
Part b) The directrix is
`x=-1/28`

Part c) The equation is
`y^(2)= (1/7)x`

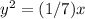
Explanation:

step 1

Find the equation of the parabola

we know that

The parabola in the graph has a horizontal axis.

The standard form of the equation of the horizontal parabola is

`(y - k)^(2)= 4p(x - h)`

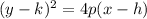
where

p≠ 0

The vertex of this parabola is at (h, k).

The focus is at (h + p, k).

The directrix is the line x= h- p.

The axis is the line y = k.

If p > 0, the parabola opens to the right, and if p < 0, the parabola opens to the left

In this problem we have that the vertex is the origin

so

(h,k)=(0,0)

substitute in the equation

`(y - 0)^(2)= 4p(x - 0)`

`y^(2)= 4p(x)`

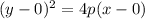
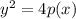
The points (7,1) and (7,-1) lies on the parabola-----> see the graph

substitute the value of x and the value of y in the equation and solve for p

`(1)^(2)= 4p(7)`

`1= 28p`

`p=1/28`

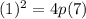
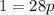
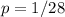
The equation of the horizontal parabola is

`y^(2)= 4(1/28)(x)`

`y^(2)= (1/7)x`

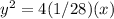
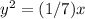
step 2

Find the focus

we know that

The focus is at (h + p, k)

Remember that

`(h,k)=(0,0)`

`p=1/28`

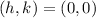
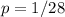
substitute

`(0+1/28,0)`

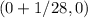
therefore

The focus is at

`F (1/28,0)`

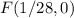
step 3

Find the directrix

The directrix is the line x = h- p

Remember that

`(h,k)=(0,0)`

`p=1/28`

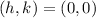
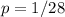
substitute

`x=0-1/28`

`x=-1/28`