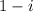Question

I need help with my algebra assignment

Answer 1

`Question 1\\1+i\\-1-i\\Question 2\\\\-1+i\\1-i`

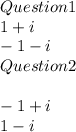
Explanation:

Complex Numbers:

Complex numbers can generally be expressed in the form:
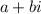`a+bi` where a and b are both real numbers, with the a part representing the real part of the complex number, and the bi representing the imaginary part.

We can also graph these numbers using the complex plane. The complex plane has the real axis where the x-axis would normally be, and the imaginary axis where the y-axis would normally be. So by this definition the "a" is what determines the horizontal position or the position on the real axis and the "b" is what determines the vertical position or the position on the imaginary axis.

I attached a diagram of the complex plane, and it's essentially the same as a normal graph, with a=x, and b=y.

Question 1:

So when a complex number lies above the real-axis, that means the imaginary part is greater than 0. When a complex numbers lies to the right of the imaginary axis, that means the real part is greater than 0.

This means we have the form:
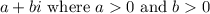`a+bi \text { where } a > 0 \text{ and } b > 0`. You can literally plug in any number for a and b, so long as it fits this. For example we can just do:
`1+i`

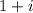
So when a complex number lies below the real-axis, that means the imaginary part is less than 0. when a complex numbers lies to the left of the imaginary axis, the real part is less than 0.

This means we have the form:
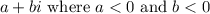`a+bi \text { where } a < 0\text{ and }b < 0`. You can plug in any real number that lies within this restriction. An example would be:

`-1-i`

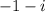
Question 2:

Above real axis and to the left of the imaginary axis means: b>0 and a<0. So we can plug in any number into the standard form that fits this restriction. an example would be:
`-1+i`

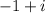
Below real axis and to the right of the imaginary axis means: b<0 and a>0. So we can plug in any number into the standard form that fits this restriction. An example would be:
`1-i`