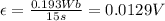Answer:
0.0129 V
Step-by-step explanation:
The magnitude of the induced emf in the circuit is given by:
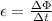
where
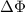 is the change in magnetic flux through the coil
is the change in magnetic flux through the coil
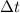 is the time interval
is the time interval
To find the change in magnetic flux, we need to find the initial flux and the final flux.
The area of the coil is
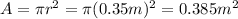
The initial magnetic field is
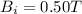
so the initial flux is
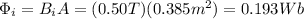
While the final flux is zero, since the coil is completely out of the magnetic field:
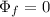
so the magnitude of the change in flux is

While the time interval is
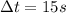
so the induced emf is