Question

Tennis balls with a 3 inch Diameter are sold in cans of three. The can is a cylinder

A)what is the volume of one tennis ball ?

B)what is the volume of the cylinder ?

C)how much space is not occupied by the tennis balls in the can?

Answer 1

Explanation:

A) The equation for the volume of a sphere is
`V=(4)/(3) \pi r^(3)`

As the diameter of each ball is 3 inches, that would mean that the radius of each is 1.5 inches.

Now we can plug our value into the equation

`V=(4)/(3) \pi (1.5)^(3)`

This would simplify to

V = 14.12716694
`in^(3)`

B) The equation for the volume of a cylinder is
`V=d\pi h`

As there are 3 balls in a container and the diameter of each is 3, that would mean that the height is 9 inches

Now we can plug in our values into the equation

`V = (3)(9)\pi`

This would mean that this equation would simplify to

`V =` 27\pi
`in^(3)`

C) To find the empty space, we must take the total volume, the volume of the cylinder, and subtract the volume of the tennis balls

This would mean that the equation would look like this

`(27\pi)-(3((4)/(3) \pi (1.5)^(3)))`

This would simplify to

42.41150082
`in^(3)` of empty space.

Answer 2

The volume of each tennis vall is 14.13 cubic inches, approximately.

The volume of each can is 63.59 cubic inches, approximately.

There are 49.46 cubic inches of empty space between the tennis balls and the cans.

Explanation:

Givens

• The diameter of each ball is 3 inches long.
• They are sold in cans of three, that is, each can contains 3 tennis balls.
• Each can has cylinder form.

First, we find the volum of each tennis ball.

Notice that they have spherical form, so their volume is defined by

`V=(4)/(3) \pi r^(3)`

Where
`r=(d)/(2)=(3 in )/(2)=1.5in`

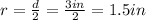
Replacing the radius and using
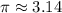`\pi \approx 3.14`, we have

`V=(4)/(3)(3.14)(1.5in)^(3)=14.13 \ in^(3)`

Therefore, the volume of each tennis vall is 14.13 cubic inches, approximately.

Assuming that the diameter of each ball is congruent with the diameter of the can, we have the volume of a cylinder defined by

`V=\pi r^(2)h`

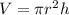
Where,
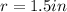`r=1.5in` and
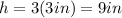`h= 3(3in)=9in`, because each can has three balls, and the height is the sum of all three diameters.

Replacing, we have

`V=3.14(1.5in)^(2) (9in)=63.59 in^(3)`

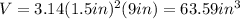
Therefore, the volume of each can is 63.59 cubic inches, approximately.

Now, notice that between the can and the tennis balls thereis empty space, because balls are spherical and cans are cylindric.

Let's find the difference between their volumes:

`V_(empy)=63.59-14.13= 49.46 in^(3)`

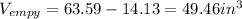
Therefore, there are 49.46 cubic inches of empty space between the tennis balls and the cans.