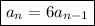Answer:
Explanation:
Step 1. Determine the common ratio
The formula for the nth term of a geometric sequence is
aₙ = a₁rⁿ⁻¹
Data:
a₁ = 4
n = 6
a₆ =31 104
Calculation:
31 104 = 4r⁵
r⁵ = 7776
![r = \sqrt [5]{7776}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kn3i78ov6d8pxg24uw0yjcg09p7khyxu1e.png)
r = 6
aₙ = 4(6)ⁿ
Step 2. Determine the recursive formula.
aₙ = 4(6)ⁿ
aₙ₋₁ = 4(6)ⁿ⁻¹
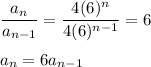
The recursive formula for the series is