Question

A positive charge, q1, of 5 µC is 3 × 10–2 m west of a positive charge, q2, of 2 µC. What is the magnitude and direction of the electrical force, Fe, applied by q1 on q2? magnitude: 3 N direction: east magnitude: 3 N direction: west magnitude: 100 N direction: east magnitude: 100 N direction: west

Answer 1

Magnitude 100 N, direction East

Step-by-step explanation:

Edge test answer confirmed

Answer 2

magnitude: 100 N direction: east

Step-by-step explanation:

The electrostatic force between two charges is given by

`F=k(q_1 q_2)/(r^2)`

where

k is the Coulomb's constant

q1 and q2 are the two charges

r is the separation between the charges

In this problem, we have

`q_1 = 5 \mu C = 5\cdot 10^(-6) C`

`q_2 = 2 \mu C = 2\cdot 10^(-6) C`

`r=3\cdot 10^(-2) m`

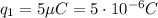
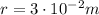
Substituting into the equation, we find the magnitude of the force

`F=(9\cdot 10^9 N m^2 C^(-2))((5\cdot 10^(-6)C)(2\cdot 10^(-6)C))/((3\cdot 10^(-2)m)^2)=100 N`

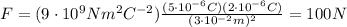
Concerning the direction, let's notice that:

- Both charges are positive, so the force between them is repulsive

- The charge q1 is west of the charge q2

- So, the force applied by q1 on q2 must be to the east (away from charge q1)