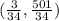Question

The equation of a parabola is given.

y=34x2−6x+15



What are the coordinates of the vertex of the parabola?



Enter your answer in the boxes.

(
,
)

Answer 1

Answer: (4,3)

He meant 3/4 not 34

Answer 2

ANSWER

`( (3)/(34) , (501)/(34) )`

Step-by-step explanation

The given parabola has equation;

`y = 34 {x}^(2) - 6x + 15`

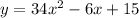
Comparing this equation to

`y = a{x}^(2) + bx + c`

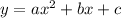
we have

a=34, b=-6 and c=15

The x-coordinate of the vertex is given by:

`x = ( - b)/(2a)`

`x = ( - - 6)/(2(34))`

`x = ( 6)/(2(34))`

`x = ( 3)/(34)`

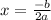
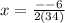
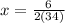
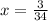
The y-coordinates of the vertex is obtained by substituting the x-value of the vertex into the equation:

`y = 34( { (3)/(34) })^(2) - 6( (3)/(34)) + 15`

`y = { (9)/(34) } - (18)/(34)+ 15`

`y = (501)/(34)`

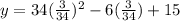
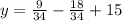
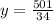
The vertex is

`( (3)/(34) , (501)/(34) )`