Answer:
Option A. (4,4)
Explanation:
step 1
Find the slope of the line k
we know that
If two lines are perpendicular, then the product of their slopes is equal to -1
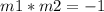
The slope of the given line is

so
The slope of the line k is

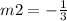
step 2
Find the equation of the line k
The equation of the line into point slope form is equal to

we have
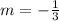

substitute the values
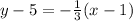
step 3
Verify if the line k pass through the given points
Remember that
If the line passes through a point, then the value of x and the value of y of the point must satisfy the equation of the line
Verify each case
case A) (4,4)
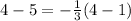
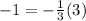
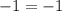 ----> is true
----> is true
therefore
The line k pass through the point (4,4)
case B) (-2,-5)
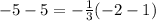
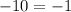 -----> is not true
-----> is not true
therefore
The line k not pass through the point (-2,-5)
case C) (3,6)
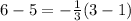
 -----> is not true
-----> is not true
therefore
The line k not pass through the point (3,6)
case D) (9,-1)
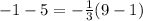
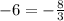 -----> is not true
-----> is not true
therefore
The line k not pass through the point (9,-1)