Question

Which conic section is represented by the equation shown below?


`2x^2-9x+4y^2+8x=16`

A. Parabola
B. Ellipse
C. Circle
D. Hyperbola

Answer 1

Answer: Option B. Ellipse

`((x-(1)/(4))^2)/((129)/(16))+((y-0)^2)/((129)/(32))=1`

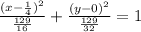
Explanation:

To know what type of conic section the function is

`2x ^ 2-9x + 4y ^ 2 + 8x = 16` we must simplify it.

`2x ^ 2-9x + 4y ^ 2 + 8x = 16\\\\2x^2 -x +4y^2 =16`

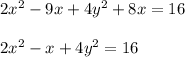
complete the square of the expression:

`2x ^ 2 -x\\\\\\2(x^2 -(1)/(2)x)\\\\2(x^2-(1)/(2)x +(1)/(16))-2(1)/(16)\\\\2(x-(1)/(4))^2 -(1)/(8)`

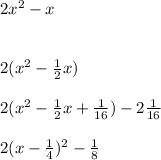
So we have

`2(x-(1)/(4))^2 -(1)/(8)+4y^2 =16\\\\2(x-(1)/(4))^2+4y^2 =(129)/(8)\\\\(8)/(129)[2(x-(1)/(4))^2] +(8)/(129)[4y^2] =1\\\\(16(x-(1)/(4))^2)/(129)+(32(y-0)^2)/(129)=1`

`((x-(1)/(4))^2)/((129)/(16))+((y-0)^2)/((129)/(32))=1`

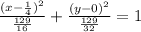
We know that the general equation of an ellipse has the form

`((x-h)^2)/(a^2) +((y-k)^2)/(b^2)=1`

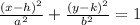
Then the equation

`((x-(1)/(4))^2)/((129)/(16))+((y-0)^2)/((129)/(32))=1`

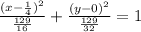
is an ellipse with center
`((1)/(4), 0)`

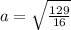`a =\sqrt{(129)/(16)}` and
`b=\sqrt{(129)/(32)}`

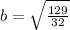
Observe the attached image