Question

the terminal side of theta passes through the point (-5,-6). what is the exact value of cos theta in simplified form?

Answer 1

`\cos( \theta) = - (5√(61))/( 61 )`

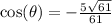
Step-by-step explanation

The given point is (-5,-6).

This implies that ,

`\tan( \theta) = (6)/(5)`

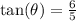
Hence opposite=6 units and adjacent=5 units.

The hypotenuse is,

`= \sqrt{ {5}^(2) + {6}^(2) } = √(61)`

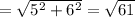
Since the terminal side is in the third quadrant, the cosine ratio is negative.

`\cos( \theta) = - (adjacent)/(hypotenuse)`

`\cos( \theta) = - (5)/( √(61) )`

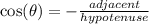
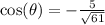
Rationalize the denominator,

`\cos( \theta) = - (5√(61))/( 61 )`

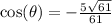
The correct choice is C.