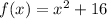Answer:
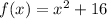
Explanation:
By the conjugate rule, if -4i is a root, then so is +4i. So we have 2 roots, thus, we have a second degree polynomial (namely, a quadratic). If
x = -4i, then
x + 4i is a root.
If
x = 4i, then
x - 4i is a root.
Having (x - 4i)(x + 4i) as roots, we can now FOIL them together to get a polynomial of least degree.
FOILing gives us
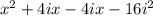
Notice that the +4ix and the -4ix cancel each other out, leaving you with
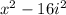
Since

we can make the substitution:
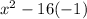
which simplifies to
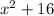
In function notation form: