Question

Need help,

plezz

What is the length of the major axis of the conic section shown below?

(x-3)^2/49 + (y+6)^2/100=1

A. 20

B. 10

C. 14

D. 7

Answer 1

Answer: A. 20

Explanation:

For the general equation of ellipse :-

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

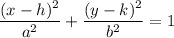
If a > b , then the length of major axis = 2a

If b> a , then the length of major axis = 2b

The given equation :
`((x-3)^2)/(49)+((y+6)^2)/(100)=1`

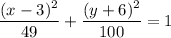
Which can be written as :

`((x-3)^2)/(7^2)+((y+6)^2)/(10^2)=1`

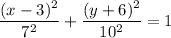
Here 10 >7 , then the length of major axis =2(10)=20 units

Answer 2

A. 20.

Explanation:

The denominators 49 and 100 are the squares of 1/2 of the lengths of the minor and major axis. The standard form is x^2/a^2 + y^2/b^2 = 1 so

a = 2 * √49 and b = 2 * √100.

The length of the major axis is therefore 2* √100

= 2 * 10

= 20 (answer).