Question

Solve for the roots in the equation below.In your final answer. Include each of the necessary steps and calculations. x^3 - 27 =0

Answer 1

Hello!

The answer is:

The equation has only one root (zero) and its's equal to 3.

`x=3`

Why?

We are working with a cubic equation, it means that there will be three roots (zeroes) for the equation.

To solve the problem, we need to remember the following exponents and roots property:

`\sqrt[n]{x^(m) }=x^{(m)/(n) }`

`(a^(b))^(c)=a^(b*c)`

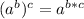
So, we are given the equation:

`x^(3)-27=0`

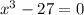
Isolating x we have:

`x^(3)=27\\\\\sqrt[3]{x^(3)}=\sqrt[3]{27}\\\\x^{(3)/(3) }=\sqrt[3]{(3)^(3) }\\\\x^{(3)/(3) }=3^{(3)/(3) }\\\\x=3`

Hence, we have that the equation has only one root (zero) and its's equal to 3.

Have a nice day!

Answer 2

x=3

Step-by-step explanation

The given equation is:

`{x}^(3) - 27 = 0`

We add 27 to both sides of the equation to get:

`{x}^(3) = 27`

We write 27 as number to exponent 3.

`{x}^(3) = {3}^(3)`

The exponents are the same.

This implies that, the bases are also the same.

Therefore

`x = 3`