Answer: 9 units.
Explanation:
Let x be the width of the rectangle .
Then, the length would be x-5.
Area of rectangle = Length x Breadth
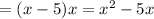
Since , The area of the rectangle is 36 units.

But width cannot be negative , so width = x= 9 units
Hence, the width of the rectangle = 9 units.